Officially, there are 1,950 coronavirus cases in the UK. Given the limits on testing, and the rapid growth in infections, the government’s own advisers believe the true number could be closer to 55,000.

These cases are not evenly distributed, and we know that London is a few weeks ahead of the rest of the country. Let’s say say London accounts for roughly half of these cases (25,000). The population of the city is roughly 8.9 million. Official advice is to avoid non-essential use of public transport and where possible avoid rush hour or work from home.

How risky is ignoring this advice? If you’re in a crowd of 100 people, what’s the probability that someone in that crowd is infected? How many people fit into a tube carriage with you? How many would you actually be exposed to?

Assume for the sake of argument your commute involves one train journey, that your fellow commuters are drawn at random from the population of the city, and that you all get on and off at the same station. Standing capacity on the most recent vintage of tube trains is about six people per square meter. A cough travels about six metres, and a sneeze about eight metres ¹.

The diameter of the circle we’re thinking about is roughly sixteen metres. A tube train is about 2.68 metres wide and 16.5 metres long, so if you stand in the middle of the carriage you’re roughly within range of every other commuter.

At this scale, a rectangle will serve for an approximate area. This gives 44.22 square metres – or at peak travel times 265 people.

The probability that any one of them is infected is (naively) , or 0.28%.

The probability that none of them are infected is 47%.

Surprising, right?

Now think about how many people you’d actually come into contact with on a commute – walking through stations, switching trains, coming into the office. How many people might you ‘meet’ in a day? Even if you travel when our example train is at half capacity – 133 people – there’s a 31% chance one of them will be sick.

You can play with the maths yourself if you want: the formula is , where x is the number of people you meet ². At about 246 people, the probability hits 50%.

Obviously you may only be exposed to some of these people for a short time, and just because someone is infected doesn’t mean they will pass the disease on to you. This is just the probability of passing someone with coronavirus.

Still, probably best to follow the official advice. And if you can, work from home.

Header image courtesy of Clement127 on Flickr, used under a creative commons license. 

1. The probability of being hit by droplets surely decreases with distance, and obscuration by fellow passengers. As we’re thinking about infected people within a potentially viable range, let’s set this to one side.
2. Technically, this should be a random draw without replacement as we’re looking for specific infected people within a population rather than observing simultaneous and independent trials. Fortunately, the difference between 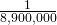and 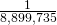is so small as to not be worth worrying about